Zanim padnie odpowiedź na tytułowe pytanie, warto na chwilę spojrzeć wstecz. Absolwenci 2025 rozpoczynali naukę w szkołach średnich w roku 2021 (liceum) lub 2020 (technikum), czyli ważny materiał z ostatnich klas szkoły podstawowej poznawali w trybie zdalnym.

 

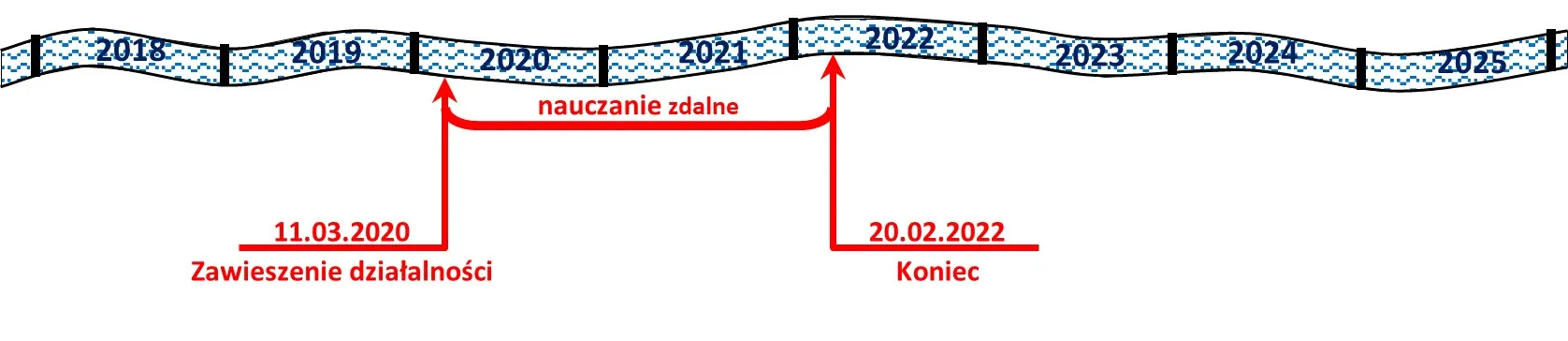
Aby złagodzić negatywny wpływ szczególnych warunków, w jakich było prowadzone kształcenie w okresie stanu zagrożenia epidemicznego i stanu epidemii wywołanej wirusem SARS-CoV-2, wprowadzono pewne ograniczenia w obszarze umiejętności diagnozowanych na egzaminie maturalnym. Aneksy CKE do informatorów zawęziły zakres kompetencji, które miały być przedmiotem badania na maturach w 2023 i 2024 roku. Zmniejszono także maksymalną liczbę punktów możliwych do uzyskania na maturze podstawowej z planowanych 50 do 46.

Matura podstawowa w roku 2025 zostanie przeprowadzana z użyciem arkusza egzaminacyjnego zawierającego:

• 20–25 zadań zamkniętych, za rozwiązanie których będzie można uzyskać 25 punktów,
• 7–14 zadań otwartych, dających możliwość uzyskania również 25 punktów.

Matura rozszerzona bez zmian – nadal do zdobycia będzie 50 punktów.

Sporo zmian, mniej lub bardziej istotnych, wprowadzono w podstawie programowej 2024, która jest również wykazem umiejętności, jakie będą diagnozowane na maturze. Poniżej zamieszczono wykaz najważniejszych zmian, utworzony przez porównanie zakresu podstawy programowej obowiązującej od 1 września 2024 r. z wymaganiami egzaminacyjnymi opublikowanymi w Aneksach.

 

Najważniejsze zmiany w umiejętnościach maturalnych od 2025 r.

I. Liczby rzeczywiste

Zakres podstawowy

• Dodano przykład zadania dotyczącego umiejętności przeprowadzania prostych dowodów. Jest nim dowód własności: jeśli liczba przy dzieleniu przez 4 daje resztę 3, to nie jest kwadratem liczby całkowitej. Warto zauważyć, że jedną z najprostszych strategii przeprowadzenia tego dowodu jest rozumowanie nie wprost. Ten typ wnioskowania jest trudny dla maturzysty, którego umiejętności matematyczne są na średnim lub niskim poziomie.
• Poszerzono wykorzystanie własności potęgowania i pierwiastkowania w sytuacjach praktycznych do obliczania procentów składanych nie tylko z kapitalizacją roczną.
• Usunięto nierówności typu 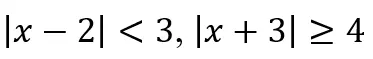 (nierówności z wartością bezwzględną pojawiają się w zakresie rozszerzonym w dziale III).

 

II.Wyrażenia algebraiczne

Zakres podstawowy

• Usunięto umiejętności dotyczące wielomianów i wyrażeń wymiernych:
• Rozkładanie wielomianów na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów.
• Dodawanie i odejmowanie wyrażeń wymiernych.

Pierwsza z tych zmian powoduje, że znaczna część zadań o wielomianach znajdujących się w podręcznikach, zbiorach zadań, a także w arkuszach maturalnych będzie wyłączona z matury na poziomie podstawowym, w tym popularne równania wielomianowe typu:  (2024 r.). Druga zmiana może natomiast nieco utrudnić nauczanie fizyki i innych przedmiotów, w których umiejętność przekształcania wzorów może być przydatna.

Zakres rozszerzony

• Ograniczono umiejętność znajdowania pierwiastków wielomianu o współczynnikach całkowitych do pierwiastków, które są liczbami całkowitymi ‒ pominięto pierwiastki wymierne.
• Dodano znajomość wzorów .
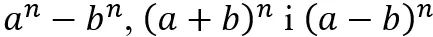• Z zakresu podstawowego przeniesiono tu rozkład wielomianów na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów, a także dodawanie i odejmowanie wyrażeń wymiernych, np.: .
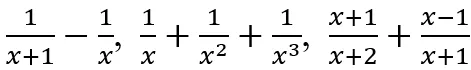• Pojawił się nowy zapis:
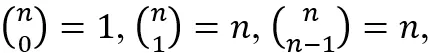
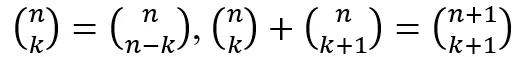
  • Uczeń stosuje podstawowe własności trójkąta Pascala oraz następujące własności współczynnika dwumianowego (symbolu Newtona):    

 

III. Równania i nierówności

Zakres podstawowy

• Doprecyzowano brzmienie pkt.1., mówiącego o przekształcaniu równań i nierówności w sposób równoważny, poprzez dodanie przykładu równania: .
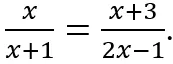• Ograniczono zakres umiejętności interpretowania równań i nierówności sprzecznych oraz tożsamościowych do tych, które są liniowe.
• Pozostaje umiejętność rozwiązywania równań wielomianowych postaci 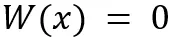 dla wielomianów doprowadzonych do postaci iloczynowej, natomiast usunięto zapis mówiący o równaniach, które dają się doprowadzić do postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub metodą grupowania. Warto zauważyć, że mimo tego można rozwiązywać równania typu 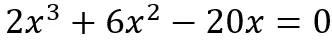, gdyż można posłużyć się wyłączaniem jednomianu przed nawias (umiejętność II.3.). Poza zakresem podstawowym jest natomiast wyłączanie np. dwumianu przed nawias.
• W nowej podstawie programowej nie ma już rozwiązywania równań wymiernych postaci 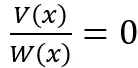, gdzie wielomiany  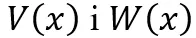są w postaci iloczynowej. Zniknie zatem
  z arkuszy maturalnych kolejny popularny typ zadań.

Zakres rozszerzony

• Pojawia się tu usunięta z zakresu podstawowego umiejętność rozwiązywania równań wielomianowych postaci 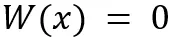 dla wielomianów, które dają się doprowadzić do postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub metodą grupowania.
• Zmienił się typ równań i nierówności wymiernych, które uczeń powinien na poziomie rozszerzonym umieć rozwiązywać. Obecnie mówi się o równaniach i nierównościach wymiernych, które dadzą się sprowadzić do równania lub nierówności liniowej lub kwadratowej.
• Zrezygnowano z precyzowania za pomocą przykładów stopnia trudności równań i nierówności z wartością bezwzględną, które uczeń powinien umieć rozwiązywać.
• Zmieniono zapis dotyczący analizowania równań i nierówności (liniowych lub kwadratowych) z parametrem. Zamiast sformułowania „Uczeń podaje warunki, przy których rozwiązania mają żądaną własność” jest: „Uczeń podaje warunki, przy których rozwiązania mają określone znaki bądź należą do określonego przedziału”.
• Wrócił zapis z poprzedniej podstawy programowej (nieobecny w Aneksie):
• Uczeń rozwiązuje równania wielomianowe, które dają się doprowadzić do równania kwadratowego, w szczególności równania dwukwadratowe.
• Z zakresu podstawowego przeniesiono rozwiązywanie równań wymiernych postaci 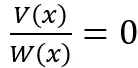, gdzie wielomiany  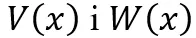 są w postaci iloczynowej.

IV. Układy równań

Zakres podstawowy ‒ bez zmian.

Zakres rozszerzony

• Zmieniono opis dotyczący typu układów równań. Uczeń powinien umieć rozwiązywać układy równań liniowych i kwadratowych z dwiema niewiadomymi, które można sprowadzić do równania kwadratowego lub liniowego, a które nie są trudniejsze niż 

 

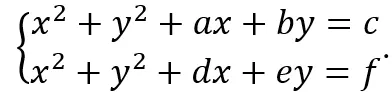
V. Funkcje

Zakres podstawowy

• Usunięto umiejętność szkicowania na podstawie wykresu funkcji wykresów funkcj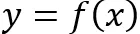i  i .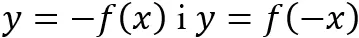
• Dodano umiejętność posługiwania się funkcją 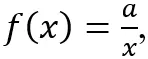, w tym jej wykresem, do opisu i interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi, również w zastosowaniach praktycznych.

Zakres rozszerzony

• Z zakresu podstawowego przeniesiono tu rysowanie wykresu funkcji 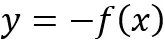 oraz 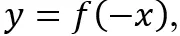 gdy dany jest wykres funkcji .
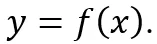• Usunięto umiejętność rysowania wykresu funkcji 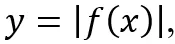 gdy dany jest wykres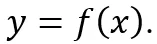 
• Dopisano dwie nowe umiejętności:
  • Uczeń posługuje się złożeniami funkcji.
  • Uczeń dowodzi monotoniczności funkcji zadanej wzorem, jak w przykładzie: wykaż, że funkcja 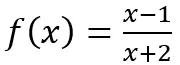 jest monotoniczna w przedziale .

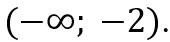VI. Ciągi

Zakres podstawowy

• Dodano umiejętność obliczania początkowych wyrazów ciągów określonych rekurencyjnie.

Zakres rozszerzony

• Tu także wprowadzono jedną zmianę, ustalając, że uczeń przy obliczaniu granic powinien umieć stosować twierdzenie o trzech ciągach.

 

VII. Trygonometria

Zakres podstawowy

• Rozwiązywanie trójkątów ograniczono do trójkątów prostokątnych.
• W Warunkach i sposobie realizacji podstawy programowej jest informacja, że uczniowie powinni umieć korzystać z tablic matematycznych i kalkulatora w dwóch celach: wyznaczania przybliżonych wartości funkcji trygonometrycznych danego kąta oraz określenia kąta, dla którego funkcja trygonometryczna osiąga określoną wartość.

Zakres rozszerzony

• Jedyna zmiana to wykreślenie przykładu równania trygonometrycznego, które miało wyznaczać stopień trudności takich równań.

 

VIII. Planimetria

Z obu zakresów wykreślono twierdzenie o dwusiecznej kąta i twierdzenie o kącie między styczną a cięciwą.

Zakres podstawowy

• Istotną zmianą, zwłaszcza w kontekście matury, jest umieszczenie w nowej podstawie programowej umiejętności przeprowadzania dowodów geometrycznych.
• Drobniejszą zmianą jest dodanie ortocentrum do punktów szczególnych w trójkącie, które uczeń powinien umieć wskazać.

Zakres rozszerzony

• Umiejętność przeprowadzania dowodów geometrycznych przeniesiono do zakresu podstawowego.

IX. Geometria analityczna na płaszczyźnie kartezjańskiej

Z obu zakresów wykreślono obliczanie odległości punktu od prostej.

Zakres podstawowy

• Dodano umiejętność posługiwania się równaniem prostej w postaci ogólnej.
• Usunięto wyznaczanie równania prostej prostopadłej do zadanej prostej i prostej stycznej do zadanego okręgu. Niemniej jednak w punkcie 1. zapisana jest umiejętność rozpoznawania wzajemnego położenia dwóch prostych na płaszczyźnie na podstawie ich równań, więc stosowanie kryterium prostopadłości (iloczyn współczynników kierunkowych równy ‒1) jako narzędzia do rozstrzygania o takim właśnie położeniu mieści się w zakresie podstawowym.

Zakres rozszerzony

• Z zakresu podstawowego przeniesiono tu wyznaczanie równania prostej prostopadłej do zadanej prostej i prostej stycznej do zadanego okręgu.
• Usunięto umiejętność znajdowania punktów wspólnych prostej i paraboli, ale zostawiono umiejętność znajdowania punktów wspólnych prostej i okręgu.
• Dodano umiejętność znajdowania punktów wspólnych dwóch okręgów.
• Poszerzono zakres umiejętności związanych z wektorami o dodawanie wektorów i mnożenie wektora przez liczbę. Oba te działania uczeń powinien umieć wykonywać zarówno analitycznie, jak i geometrycznie.

 

X. Stereometria

Zakres podstawowy

• Z zakresu rozszerzonego przeniesiono umiejętność posługiwania się pojęciem kąta dwuściennego między półpłaszczyznami oraz rozpoznawanie i obliczanie miar kątów między ścianami w graniastosłupach i ostrosłupach.
• Dodano umiejętności dotyczące brył obrotowych: rozpoznawanie w walcach i w stożkach kątów między odcinkami oraz kątów między odcinkami i płaszczyznami (np. kąt rozwarcia stożka, kąt między tworzącą a podstawą), obliczanie miary tych kątów, obliczanie objętości i pola powierzchni walca, stożka i kuli.
• Umiejętność wykorzystywania zależności między objętościami brył podobnych rozszerzono na dowolne bryły, bez zawężania do graniastosłupów i ostrosłupów.

Zakres rozszerzony

• Usunięto umiejętności posługiwania się pojęciem kąta dwuściennego między półpłaszczyznami oraz rozpoznawania i obliczania miar kątów między ścianami w graniastosłupach i ostrosłupach w związku z przeniesieniem ich do zakresu podstawowego.
• Usunięto umiejętność określania, jaką figurą jest dany przekrój prostopadłościanu płaszczyzną

 

XI. Kombinatoryka

Zakres podstawowy – bez zmian.

Zakres rozszerzony

• Do umiejętności stosowania współczynnika dwumianowego dopisano również stosowanie jego własności.

 

XII. Rachunek prawdopodobieństwa i statystyka

Z obu zakresów wykreślono obliczanie odchylenia standardowego zestawu danych.

Zakres podstawowy – prócz powyższej uwagi bez zmian.

Zakres rozszerzony

• Nowym elementem jest umiejętność stosowania wzoru Bayesa.

 

XIII. Optymalizacja i rachunek różniczkowy

Zakres podstawowy ‒ bez zmian.

Zakres rozszerzony

• Dodano umiejętność stosowania własności Darboux do uzasadniania istnienia miejsca zerowego funkcji.
• Oprócz interpretacji geometrycznej pochodnej uczeń powinien teraz znać również interpretację fizyczną.
• Dodano umiejętność obliczania pochodnej funkcji złożonej.

 

Nowe umiejętności na maturze od 2025 r.

W omówionych zmianach niejednokrotnie anonsowano pojawienie się nowych umiejętności, które nie były zapisane w Aneksach, a zatem nie były sprawdzane na maturze w 2023 czy 2024 roku. Warto poszukać w podręcznikach, zbiorach zadań czy innych źródłach takich zadań i sprawdzić, jak radzą sobie z nimi ci, którzy w maju 2025 roku przystąpią do matury. Poniżej zamieszczone są przykłady trzech takich zadań dla zakresu podstawowego.

 

Zadanie 1.

Wykaż, że jeśli liczba przy dzieleniu przez 7 daje resztę 5, to nie jest kwadratem liczby całkowitej.

Zadanie 2.

Na przyprostokątnych AB i AC trójkąta prostokątnego równoramiennego ABC obrano odpowiednio punkty D i E tak, że odcinek DE jest równoległy do przeciwprostokątnej i dzieli trójkąt na dwie figury o równych polach. Wykaż, że |DE| = |AB|.

Zadanie 3. (Informator o egzaminie maturalnym z matematyki jako przedmiotu obowiązkowego, poziom podstawowy, od roku szkolnego 2024/2025)

Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy 𝑑 = 20 cm, wysokości 𝐻 = 25 cm i tworzącej 𝑙.

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Kąt rozwarcia stożka, którego powierzchnią boczną jest czapeczka, ma miarę (w zaokrągleniu do 1°)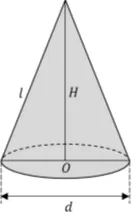

A. 44°  B. 136°  C. 22° D. 68°

 

 

Matura z matematyki w 2025 r. – łatwiejsza czy trudniejsza?

Na zakończenie warto postawić jeszcze jedno pytanie, nurtujące uczniów i nauczycieli: Czy matura podstawowa w roku 2025 będzie łatwiejsza czy trudniejsza od tych, które odbyły się w latach 2023 i 2024? Odpowiedzi mogą być dwie.

Będzie trudniejsza, bo:

• zwiększono zakres materiału, dodając niektóre umiejętności (np. dowody geometryczne, bryły obrotowe),
• nie będzie już „maturalnych pewniaków” ‒ równań wielomianowych i równań wymiernych w postaci takiej jak na ostatnich maturach,
• może zwiększyć się liczba zadań otwartych przy niezmienionym czasie trwania egzaminu,
• liczba punktów możliwych do uzyskania wzrasta z 46 do 50,
• egzaminy w poprzednich latach mogły być nieco łatwiejsze ze względu na obciążenia covidowe; teraz gdy sytuacja jest unormowana, CKE może nieznacznie „podnieść poprzeczkę”,
• w materiałach CKE z ostatnich kilku lat widać odchodzenie od zadań sprawdzających wiedzę faktograficzną i umiejętność stosowania prostych algorytmów oraz przywiązywanie coraz większej wagi do umiejętności analitycznych, myślenia logicznego, tworzenia strategii rozwiązania problemu.

Będzie łatwiejsza, bo:

• dokonano pewnych ograniczeń w zakresie opanowania niektórych umiejętności zapisanych w podstawie programowej, część bardziej złożonych umiejętności usunięto (np. obliczanie odchylenia standardowego),
• w nowej podstawie i w materiałach CKE widać tendencję do proponowania uczniom zadań sprawdzających praktyczne umiejętności, przez co mogą one być łatwiej analizowane i rozwiązywane z udziałem wiedzy i doświadczenia pozaszkolnego,
• przez ostatnich kilka lat nagromadziło się sporo materiałów ćwiczeniowych dla uczniów i metodycznych dla nauczycieli (arkusze próbne i właściwe, informator, publikacje z przykładowymi arkuszami lub z zestawami zadań, repetytoria).

Nikt nie jest w stanie udzielić teraz jednoznacznej odpowiedzi. Bardzo wiele zależy od decyzji, które zapadną podczas tworzenia zestawów egzaminacyjnych w CKE. Na to uczniowie i ich nauczyciele nie mają wpływu. Warto zatem skupić się na tym, co można ukształtować samemu lub na poziomie klasy w szkole. Ważne jest, aby nauczyciele wzbudzili u swoich podopiecznych pozytywną motywację do rzetelnych przygotowań, a uczniowie podjęli solidną pracę i bez stresu, z bogatą wiedzą przystąpili do matury. Wtedy omówione wcześniej zmiany z pewnością okażą się nie takie straszne, a radość z sukcesu będzie udziałem wszystkich.