Rzut i równia – i to naraz?!

Kiedy tylko przeczytałem zadania próbnej matury, pomyślałem, że zadanie 3 może sprawić problemy wielu uczniom. Podejrzenia okazały się słuszne: uczniowie zdobyli za nie średnio 38% punktów. Nic dziwnego. Co prawda zadania z równią pochyłą i zadania z rzutem poziomym to niemal pewniaki, rzadko się zdarza, że jedno i drugie zagadnienie spotkamy w jednym zadaniu.

Jak zawsze, zaczynamy od wyobrażenia sobie zjawiska i przypomnienia odpowiednich praw, ale nie chodzi o formalne brzmienie, tylko o prawa w działaniu; o to, jak wyjaśniają przebieg zjawisk.

• Zastosuj zasadę niezależności ruchów

Zacznijmy od rzutów. Do ich opisu przydaje się zasada niezależności ruchów – w każdym z prostopadłych odcinków ruch odbywa się niezależnie. Dla każdego z nich składową przyspieszenia można obliczyć na podstawie składowej siły, dla każdego można stosować wzory dotyczące ruchu prostoliniowego.

W szczególności w rzucie poziomym:

∙ w poziomie nie działa żadna siła, więc ciało porusza się jednostajnie,

∙ w pionie działa siła ciężkości, więc ciało spada swobodnie.

💡Wskazówka

Obejrzyj to w zwolnionym tempie na filmie, na przykład:

https://www.youtube.com/watch?v=zMF4CD7i3hg

• Rozkład sił na równi

A co kojarzy się z równią? Rozkład sił, składowa nadająca przyspieszenie… ale nie tym razem! W naszym zadaniu równia jest potrzebna tylko do stwierdzenia, że punkty początku i końca ruchu leżą na odpowiednio nachylonej prostej, a więc odległość przebyta w pionie i odległość przebyta w poziomie są w pewnej proporcji.

Szczegóły znajdziesz w ramce.

• Korzystaj z karty wzorów

A ponieważ w rozwiązaniu pojawia się równanie kwadratowe, to warto wspomnieć, że w karcie wzorów znajdują się „wzory na deltę” oraz własności logarytmów, ale jest to Easter egg – ukryły się wśród wiadomości z chemii i nawet nie zostały wspomniane w spisie treści. Warto więc o nich pamiętać.

Obrotowy? Prawie jak postępowy!

Bryła sztywna to dział, który zawsze sprawia problemy. Nic dziwnego, że także zadanie 4.2. okazało się trudne dla wielu uczniów. Jego średni wynik to zaledwie 35%, ledwo ponad 1/3.  Tymczasem wystarczy rozumieć, co się tu dzieje, i znać wzory na… ruch postępowy.

💡 Wskazówka: Naucz się dostrzegać podobieństwa między ruchem postępowym a ruchem obrotowym – to klucz do efektywnego rozwiązywania zadań.

Sonda kosmiczna i karta wzorów

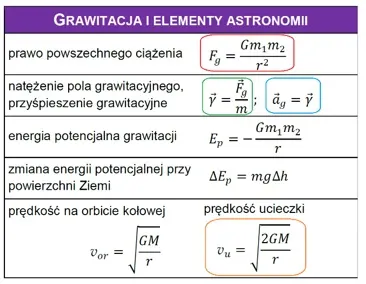
Zadanie 5.1. rozwiązało poprawnie 55% uczniów. Nie było więc może bardzo trudne, ale warto o nim powiedzieć, bo na jego przykładzie widzimy, w jaki sposób zaoszczędzić sporo czasu, korzystając sprawnie z karty wzorów (kolory odwołują się do ramek, które dorysowałem we fragmencie karty wzorów poniżej):

• dowiadujemy się, że przyspieszenie grawitacyjne to to samo, co natężenie pola grawitacyjnego,
• na natężenie pola mamy wzór, w którym występuje siła grawitacji,
• wzór na tę siłę jest piętro wyżej,
• a z kolei niżej znajdziemy wzór na prędkość ucieczki.

Jak rozwiązać zadanie?

 Trzeba wiedzieć, o co w tych wzorach chodzi, a nie tylko zauważać podobne symbole, bo ten sam symbol może mieć różne znaczenia, a co więcej – tę samą wielkość można oznaczać różnie.

W naszym wypadku wzór na siłę grawitacji zawiera symbole  i , ale

• jeden z nich oznacza masę planety, czyli to samo, co M we wzorze na prędkość ucieczki,
• drugi oznacza masę ciała na planecie, czyli to samo, co m we wzorze na natężenie pola.

Czy to nie dziwne, że w tym wzorze nie ma ani stałej grawitacji, ani masy planety? Przecież powinny one mieć wpływ na przyspieszenie grawitacyjne. Rzeczywiście powinny i mają, tylko że są ukryte w prędkości ucieczki, która od nich przecież zależy.

Na koniec powiedzmy to jeszcze raz: obliczenia są krótsze i prostsze, gdy korzystamy z gotowych wzorów z karty wzorów, ale trzeba dobrze rozumieć, o czym w tych wzorach mowa. Symbole nie są podpisane, bo karta ma służyć upewnieniu się albo przypomnieniu, ale nie pozwoli nauczyć się wszystkiego w czasie egzaminu.

Sonda daleko od planety, uczeń blisko rozwiązania

Zadanie 5.2. należało do kilku rozwiązanych najsłabiej, uczniowie zdobyli średnio 26% procent punktów. Tymczasem można je było rozwiązać w pamięci (oczywiście i tak potem trzeba te obliczenia zapisać!).

Jak rozwiązać zadanie?

Trzeba  wiedzieć, że:

• sonda wystrzelona z planety z prędkością równą prędkości ucieczki oddala się z rozpędu (bez włączonych silników) na bardzo dużą odległość, ale w tej bardzo dużej odległości praktycznie się zatrzymuje,
• energia kinetyczna jest proporcjonalna do kwadratu prędkości.

Morał stąd bardzo optymistyczny: czasami rachunki mogą być bardzo proste.

Soczewki – nietrudne, ale mało typowe

Zadanie 8 dotyczyło biegu promienia światła przez dwie soczewki.

Jak rozwiązać zadanie?

Jeśli w zadaniu masz uzupełniać rysunek, najpierw szkicuj na brudno. Naszkicujmy w brudnopisie bieg promienia światła.

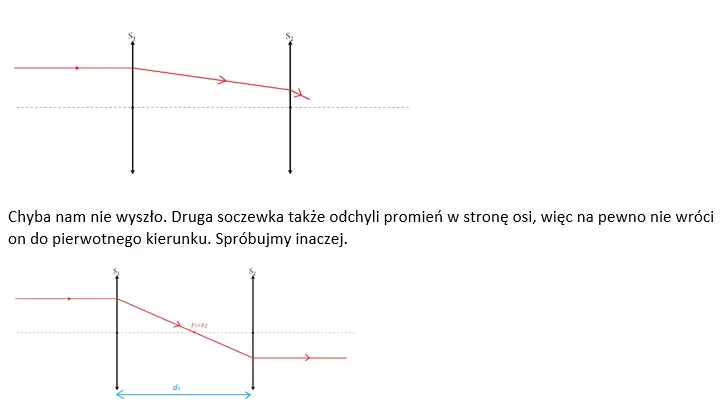
Teraz wszystko się zgadza. Od razu zauważamy też, że punkt przecięcia promienia z osią optyczną to ognisko lewej soczewki. Na tym przecież polega ognisko, że skupiają się w nim załamane promienie, które wcześniej biegły równolegle do osi soczewki.

Jest to również ognisko prawej soczewki. Jeśli nie pamiętamy, co się dzieje z promieniami wychodzącymi z ogniska po załamaniu w soczewce, to możemy sobie wyobrazić bieg światła w przeciwną stronę, od prawej do lewej.

Mamy więc ogniska.  A jak obliczyć odległość \left.\mleft.d\mright.\right._{\mleft.0\mright.} d0  między soczewkami? Jest ona równa sumie ogniskowych soczewek, a ogniskowe możemy obliczyć na podstawie ich zdolności skupiających.

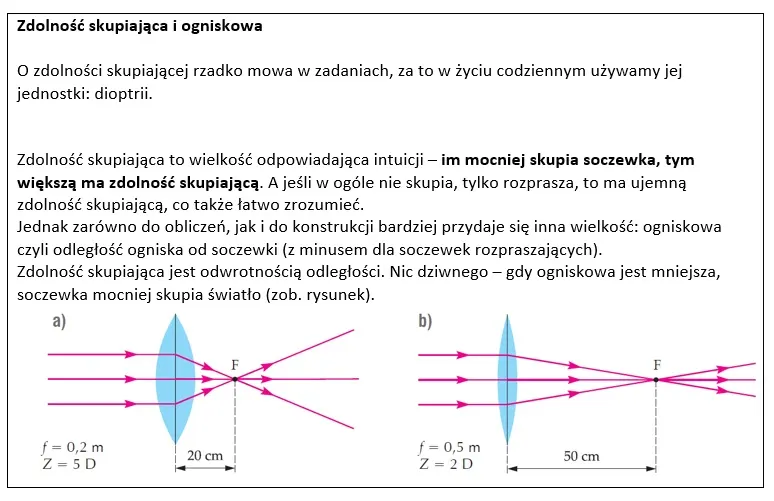
I już! Trzy punkty do przodu!

Kolejny punkt dostaniemy natychmiast za zadanie 8.2., jeśli tylko nie wpuścimy się w obliczenia. Wystarczy proste rozumowanie: dwie złączone soczewki skupiające skupiają mocniej niż każda z osobna. Tak więc soczewka zdolność skupiająca Z₃ jest większa niż każda z Z₁ i Z₂, a dla ogniskowych zależność jest odwrotna. Wybieramy odpowiedź A.

Wyniki niestety nie były zbyt wysokie: średnio 40% za część 8.1 i tylko 34% za część 8.2. A przecież zadanie 8.2 powinno być znacznie łatwiejsze. Tyle tylko, że nie było typowe. Morał jest taki, że trzeba myśleć nie „jak to się liczyło”, ale „co się dzieje”. Nie trzeba się bać, że nie rozwiązywaliśmy nic podobnego ani zastanawiać nad wzorem na ogniskową układu soczewek. Wystarczy zdroworozsądkowa obserwacja, że dwie soczewki skupiające skupiają mocniej niż jedna.

Gaz doskonały − czasami trzeba wrócić do podstaw

Po to jest równanie Clapeyrona, żebyśmy mogli zajmować się makroskopowymi wielkościami jak temperatura czy ciśnienie, a nie zastanawiali się za każdym razem nad prędkościami cząsteczek albo ich zderzeniami ze ściankami naczynia.

Trzeba jednak wiedzieć, jakie informacje o cząsteczkach dają nam te wielkości. Choćby po to, żeby rozumieć, że nie ugotujemy się w jonosferze. Albo po to, żeby rozwiązać zadanie 12.1.

Jak rozwiązać zadanie?

Początek jest łatwy: „cząsteczki poruszają się szybciej” oznacza wzrost temperatury, więc pasują przemiany 1→2 oraz 3→1. Co jednak z częstotliwością uderzeń?

W przemianie 1→2 ciśnienie jest stałe. A przecież ciśnienie wynika z uderzeń cząsteczek o ścianki naczynia. Skoro cząsteczki uderzają z większą prędkością, to muszą uderzać rzadziej, żeby te dwa czynniki się redukowały i ciśnienie się nie zmieniało.

Mamy więc odpowiedź. Na szczęście nie musimy rozważać przemiany 3→1, co byłoby trudniejsze, bo nie mamy do wyboru odpowiedzi „w przemianach 1→2 i 3→1”.

Silnik – myśl o tłoku w cylindrze, nie tylko o diagramie

Choć dzisiaj termodynamika jest dziedziną bardzo szeroką i o wielu zastosowaniach, to powstała jako teoria silników cieplnych. „Silnik” a nawet „cykl termodynamiczny” w zadaniu możemy sobie wyobrazić jako cylinder z poruszającym się tłokiem.

Jak rozwiązać zadanie?

Gaz pobiera ciepło, potem je oddaje, ale nie całe, bo część zamienia się w pracę. I samo to stwierdzenie pozwala wybrać odpowiedź w zadaniu 12.2., jeśli tylko pamiętamy, że pole wewnątrz wykresu równe jest pracy netto.

A jak obliczyć sprawność silnika w zadaniu 12.3? Tutaj wcześniejsze rozwiązanie zadania 12.2 będzie pomocne, bo przypomni nam, że praca to różnica między ciepłem pobranym a oddanym. Nie musimy więc pracowicie liczyć kratek. W przemianie adiabatycznej nie ma przepływu ciepła (tak ją przecież definiujemy), więc wystarczy obliczyć ciepło pobrane w przemianie 1→2 i ciepło oddane w przemianie 2→3.

Podsumowanie

Czy matura z fizyki jest trudna?  Pamiętaj, że to nie tylko test wiedzy, ale też umiejętność logicznego myślenia i rozumienia zjawisk.

• Nie skupiaj się wyłącznie na wzorach – zastanów się, co naprawdę dzieje się w danym zadaniu.
• Zadania nietypowe często okazują się proste.
• Szkicuj, analizuj i stosuj analogie.

Powodzenia!