Analiza wyników próbnej matury z matematyki na poziomie podstawowym przygotowanej przez Nową Erę , przyniosła wiele interesujących obserwacji. Część z nich potwierdza, świetnie znane problemy, występujące od wielu lat, aczkolwiek niektóre mogą być ciekawe, w kontekście przygotowań do matury w 2025 roku i w latach następnych, uwzględniających nową, uproszczoną podstawę programową. W artykule przedstawię najbardziej problematyczne zadania dla uczniów. Większość z nich zostało wykonane poprawnie przez mniej niż połowę piszących, a niektóre zostały rozwiązane prawidłowo tylko przez 15% abiturientów.
Próbna matura z matematyki 2025 — analiza najtrudniejszych zadań
Usuwanie niewymierności z mianownika przy pomocy wzorów skróconego mnożenia – jeden z najczęstszych problemów na maturze z matematyki

Usuwanie niewymierności z mianownika przy pomocy wzorów skróconego mnożenia jest zadaniem, które od wielu lat stwarza problemy na maturze z matematyki. Wykonało je mniej niż połowa tegorocznych maturzystów. Uczniowie na zakresie podstawowym często nie „czują” tych wzorów i ich unikają.
W wielu miejscach, gdzie można je zastosować, wolą je ominąć np. w działaniach na wyrażeniach algebraicznych, równaniach kwadratowych, dowodach algebraicznych. Niestety ten typ zadania bezwzględnie wymaga ich zastosowania.
Rozwiązanie
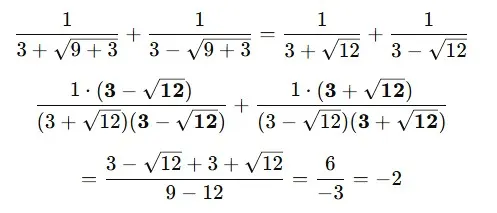
Warto bardzo dokładnie przeanalizować zastosowanie wzoru skróconego mnożenia:
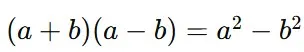
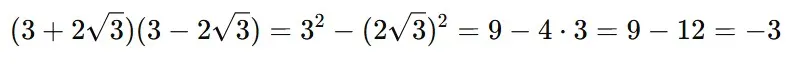
W celu dokładnego poćwiczenia tego zagadnienia warto zapoznać się z poniższym materiałem video:
Dowód algebraiczny — jak unikać błędów na maturze z matematyki?
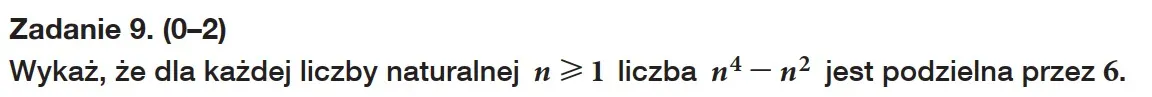
Niesłychanie problematycznym zagadnienie na maturze z matematyki jest umiejętność dowodzenia. Nie odnotowuje się większej niechęci do dowodów algebraicznych aniżeli do dowodów geometrycznych. Oba typy postrzegane są, jako trudne i niezrozumiałe. Uczniowie nie lubią dowodów i są to najczęściej pomijane zadania na maturze, zarówno podstawowej, jak i rozszerzonej.
Podstawa programowa traktuje umiejętność dowodzenia jako jedną z najważniejszych umiejętności. Biorąc pod uwagę zadania z lat ubiegłych, można zaobserwować schematyczność podejmowanej problematyki. Każdą umiejętność w kontekście egzaminu maturalnego można wyćwiczyć opierając się na świetnie znanych, powszechnych i znanych zagadnieniach.
Zanim przejdziemy do rozwiązania warto przypomnieć własności iloczynu kolejnych liczb naturalnych (lub całkowitych, gdyż ich również to dotyczy).
n(n+1) iloczyn dwóch kolejnych liczb naturalnych jest zawsze iloczynem liczby parzystej i nieparzystej, więc jest liczbą parzystą, czyli podzielną przez 2.
n(n+1)(n+2) iloczyn trzech kolejnych liczb naturalnych jest zawsze liczbą podzielną przez 2 i przez 3, zatem jest podzielny przez 6.q
Dzięki tym własnością, które należy pamiętać, tego typu zadania dowodowe stają się łatwe, szybkie i przystępne. Zapisujemy zatem, stosując podstawowe przekształcenia algebraiczne:
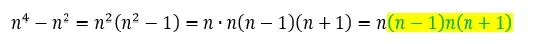

Szczerze polecam zapoznać się z problematyką dowodową. Zadania te są powtarzalne i niskim kosztem można poprawić wynik na maturze.
Własności funkcji kwadratowej — zadania, które zaskoczyły maturzystów
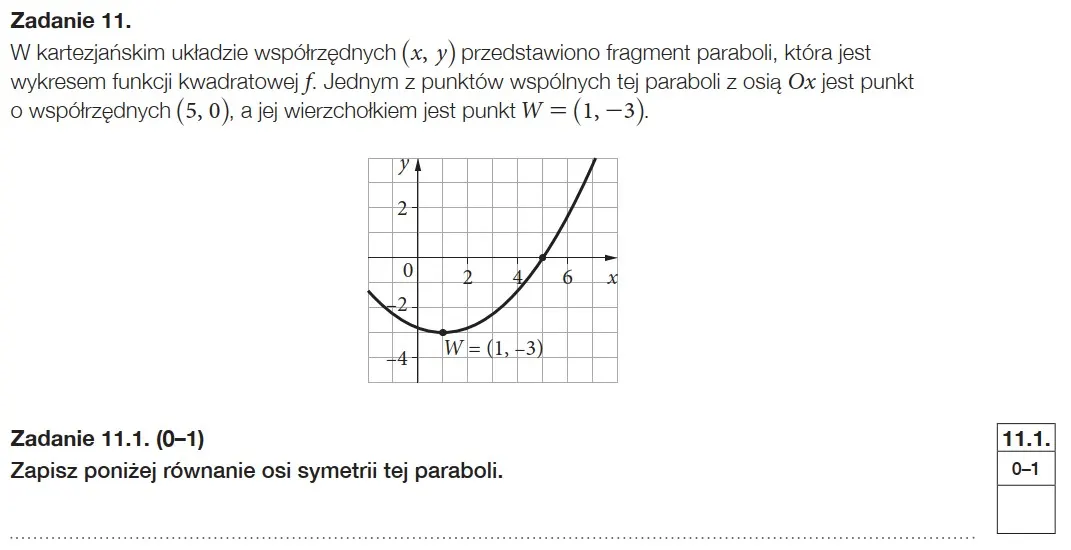
Na maturze z matematyki wielu uczniów miało duży problem z zadaniem 11, dotyczącym analizy własności funkcji kwadratowej. Zauważyć można trudności z interpretacją wykresu i powiązaniem zaobserwowanych informacji z nimi. Pojęcie równania osi symetrii często jest pomijane. Należy pamiętać, że ma ona postać x=p, gdzie p jest pierwszą współrzędną wierzchołka o współrzędnych W=(p,q). W tym przypadku p=1, zatem równaniem osi symetrii jest prosta x=1.
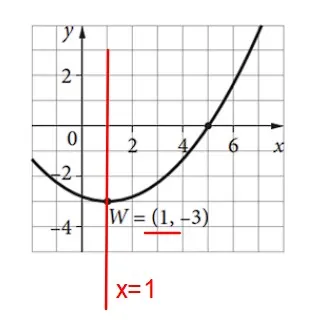
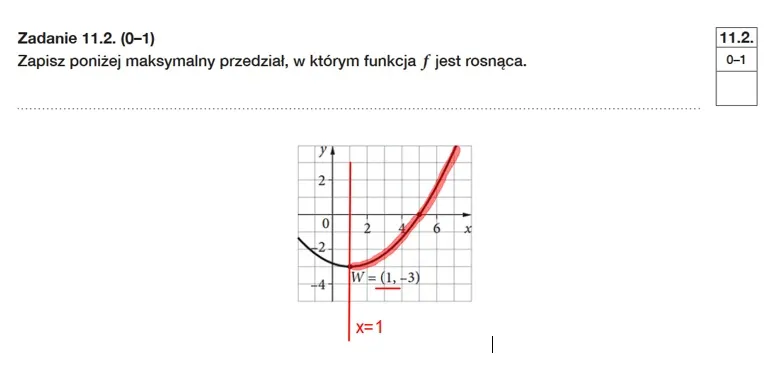
Kolejną własnością powiązaną z wierzchołkiem funkcji kwadratowej jest monotoniczność. Na rysunku zaznaczony został fragment wykresu funkcji, w którym funkcja jest rosnąca. Jest to przedział.

Kontynuując problematykę zadania. Uczniowie mają trudność z powiązaniem wyznaczonych własności dotyczących funkcji kwadratowej, z wykresem funkcji. Bardzo często bez problemu rozwiązują zadania wymagające podstawienia liczb do wzoru, wyznaczenia miejsc zerowych, współrzędnych wierzchołka, ale mają problem gdy dane trzeba odczytać bezpośrednio z wykresu i powiązać je z konkretnym wzorem funkcji kwadratowej. Dodatkowym utrudnieniem była konieczność dorysowania części wykresu, w celu odczytania drugiego miejsca zerowego.
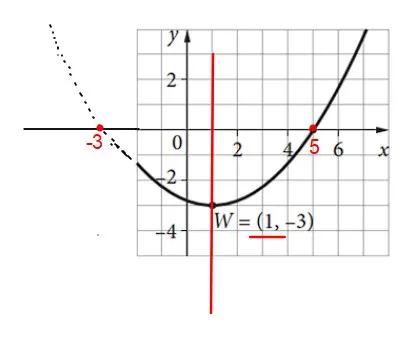

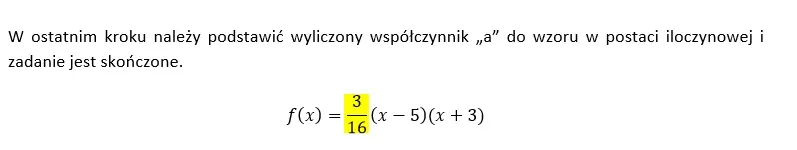
Nie jest to jedyny sposób rozwiązania tego zadania. Warto zastanowić się czy nie dałoby się inaczej do niego podejść.
W celu utrwalenia wiadomości z zakresu własności funkcji kwadratowej można zaproponować im materiał video z poniższego linku lub zapoznać się z podobnymi materiałami video z vademecum „Teraz Nowa Matura”.
Interpretacja graficzna układu równań – pułapki na maturze z matematyki

Nieoczekiwanym z mojego punktu widzenia, były trudności związane z interpretacją geometryczną układu równań liniowych. Na maturze z matematyki uczniowie co do zasady nie mają trudności z rozwiązywaniem układów równań, zarówno metodą graficzną, jak i graficzną. Szkicowanie wykresów funkcji liniowych również nie sprawia większych problemów. To zadanie jednak wymaga sprytnego podejścia analitycznego. Klasyczne podejście polegające na rozwiązaniu czterech układów równań jest czasochłonne i może prowadzić do licznych błędów w obliczu ograniczonego czasu na maturze.

Widzimy, że współczynniki „a” obu prostych mają różne znaki, więc możemy wyeliminować odpowiedzi A i D. Dodatkową trudnością będzie konieczność doprowadzenia równań, do postaci kierunkowej. Zerknijmy na odpowiedź B. Drugie równanie dzielimy obustronnie przez 2.
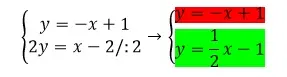
Pierwsze równanie prostej ma współczynnik a<0 i b=1, drugie równanie porstej ma współczynnik a>0 i b=-1, zatem jest to prawidłowa odpowiedź.
Ciąg arytmetyczny na maturze z matematyki — dlaczego uczniowie popełniają błędy?

Dział ciągi jest powszechnie znanym i lubianym tematem wśród maturzystów. Dziwić zatem może, że zadanie to wykonało poprawnie mniej niż połowa piszących. Nie doszukiwałbym się tu braku opanowania zagadnienia, a bardziej trudności w zrozumieniu polecenia, sformułowanego w nieprzystępny dla ucznia sposób. Tego typu zadania cały czas postrzegane są jako nowość. Próżno szukać ich w zbiorach zadań i podręcznikach. Jedynym miejscem, gdzie się pojawiają są arkusze maturalne oraz zbiory zadań maturalnych. Uczniowie nie mają doświadczenia w ich rozwiązywaniu i pomimo nawet prawidłowych obliczeń, błędnie interpretują treść i zaznaczają złą odpowiedź.
Należało skorzystać z własności dla trzech kolejnych wyrazów ciągu arytmetycznego lub geometrycznego. Szczęśliwie, okazało się, że zależność dla ciągu arytmetycznego jest prawdziwa.
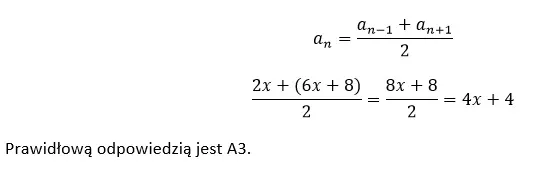
Mylące mogło być to, że odpowiedzi 1 i 2 mają sens liczbowy. Ważne w tego typu zadaniach jest to, że druga część odpowiedzi musi mieć sens w powiązaniu z pierwszą częścią. Zalecałbym zwrócenie uwagi na tego typu zadania w zbiorach zadań maturalnych.
Planimetria — jak przygotować się do trudnych zadań maturalnych?
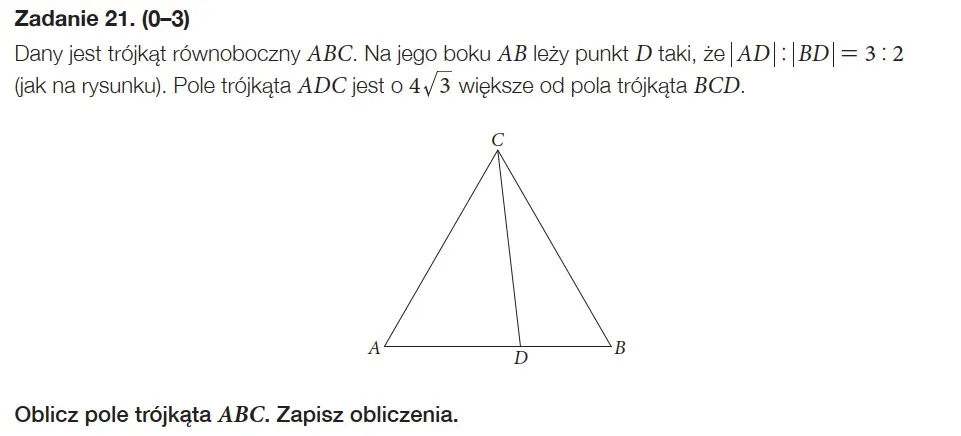
Zadania z planimetrii, zwłaszcza rozszerzonej odpowiedzi, od lat sprawiają problemy i nie inaczej było w tym przypadku. Prawidłowo rozwiązało je mniej niż 20% piszących. Cała tajemnica ukryta była w umiejętnym zastosowaniu podanych danych liczbowych i zastosowaniu wzoru na pole trójkąta z wykorzystaniem wartości funkcji trygonometrycznej sinus. Oczywiście można go znaleźć we wzorach maturalnych.
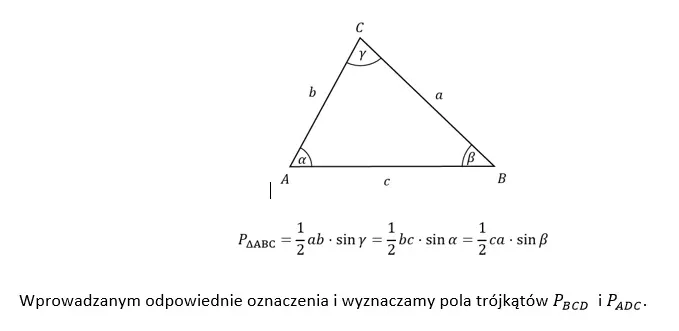
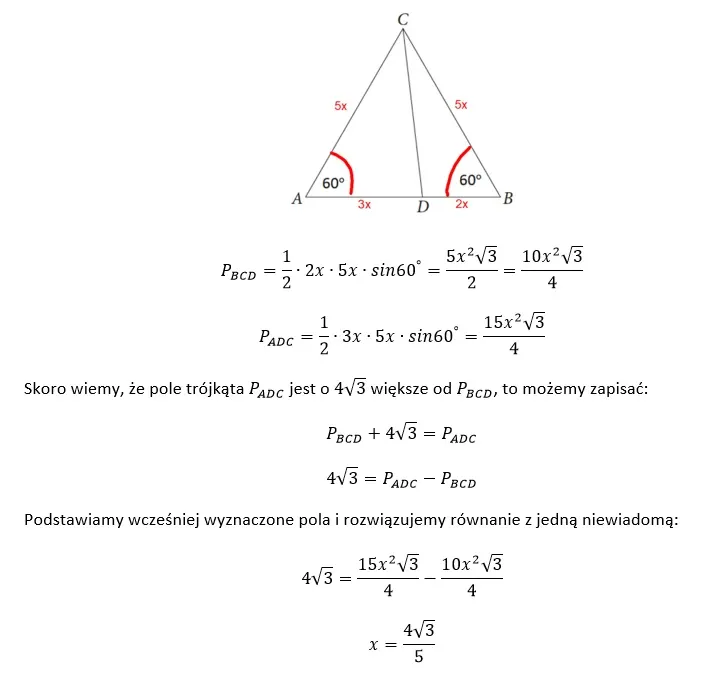
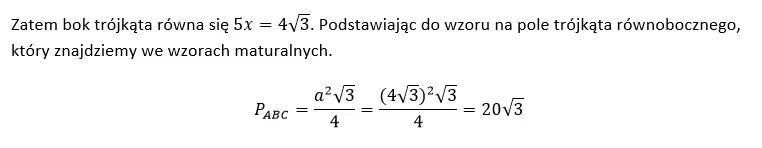
Oczywiście warto przeanalizować to zadanie pod kątem innych rozwiązań. Może będą krótsze, aczkolwiek przedstawiony sposób jest najbardziej schematycznym. Podczas rozwiązywania zadań z planimetrii, polecam stosować najbardziej schematyczne rozwiązania. Jest to pierwszy krok do wykształcenia umiejętności które umożliwią znalezienie szybszych „sprytnych rozwiązań.
Dowód geometryczny — czego boją się maturzyści?
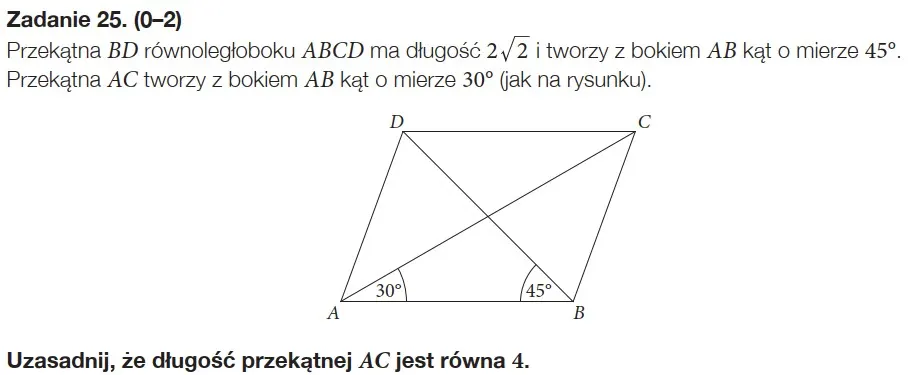
Kolejnym problematycznym zadaniem na maturze próbnej z matematyki (ku zaskoczeniu nikogo), okazał się dowód geometryczny. Wykonało go poprawnie podobna liczba osób jak zadanie 21. Z wieloletnich obserwacji, mogę podzielić się wnioskiem, że uczniowie się zwyczajnie boją tych zadań. Jak widzą w poleceniu słowo „uzasadnij”, z premedytacją je omijają. Konkretny tym zadań przedstawiony w arkusza, zwykłem nazywać „udawanym dowodem”. Polecenie mogłoby brzmieć „oblicz przekątną AC” i nic by to nie zmieniło w toku rozumowania. Jest to bardzo podobny problem jaki mieliśmy w zadaniu 21. Niska liczba poprawnych rozwiązań może sugerować, trudności z tematem planimetrii, a nie tylko umiejętności dowodzenia.
Posłużymy się tym samym twierdzeniem co w zadaniu 21.
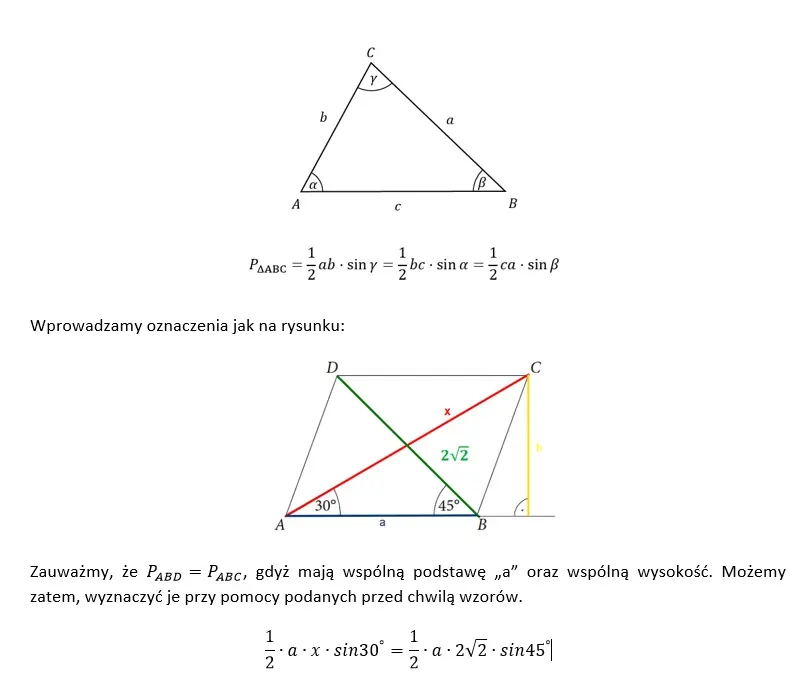

Łatwo zauważyć, że do przeprowadzenia dowodu wystarczyła podstawowa znajomość wzorów i umiejętność rozwiązywania równań. Należy zwrócić dodatkowo uwagę, że część uczniów postrzega trygonometrię, jako zagadnienie trudne i niezrozumiałe, co powoduje trudności w jej stosowaniu w planimetrii. Należy na to zwrócić uwagę podczas powtórek maturalnych.
Kombinatoryka — prosta teoria, trudna praktyka

Kombinatoryka i rachunek prawdopodobieństwa jest jednym z ulubionych działów podczas powtórek maturalnych. Wpływa na to, że są to zagadnienia mocno oderwane od pozostałych działów i wymagają niskiego progu wejścia.
W praktyce, umiejętności które potrzebujemy by zacząć rozwiązywać zadania, ograniczają się do podstawowej wiedzy z zakresu podzielności liczb oraz działań arytmetycznych. Jest to niestety również powód, który wpływa na to, że dział ten jest bagatelizowany i pomijany jako ten prostszy.
Okazuje się jednak, że nawet niezbyt skomplikowane zadanie na maturze z matematyki, może sprawić duże trudności, jak miało to miejsce w tym przypadku, gdzie poprawnie rozwiązało je mniej niż 30% piszących. Przyjrzyjmy się, co mogło być skomplikowane dla maturzystów.
Wprowadźmy sobie oznaczenie: Magda – M, Antek –A, pozostałe osoby – P .
Najtrudniejsze w zadaniu jest uświadomienie sobie, że Magdę i Antka trzeba potraktować jako jedną osobę. Skoro jest sześć miejsc, to mogą oni zająć miejsca na 5 sposobów.
MA _ _ _ _
_ MA _ _ _
_ _ MA _ _
_ _ _ MA _
_ _ _ _ MA
Jak już Magda i Antek zajmą miejsca, to następne osoba może zająć jedno z 4, następna jedno z 3, następna jedno z 2, następna jedno z 1. Co daje nam ostatecznie:
możliwości.
Pamiętać należy jednak o tym, że Magda i Antek mogą zamienić się miejscami, czyli wynik należy pomnożyć przez 2, co daje nam ostatecznie 240 możliwości, co było prawidłowym rozwiązaniem.
Warto podczas powtórek maturalnych przerobić dodatkowe zadania z zakresu kombinatoryki, by na egzaminie ustrzec się błędów.
Stereometria – co sprawia trudność na maturze z matematyki?

Jednym z najsłabiej napisanych zadań okazała się stereometria. Uczniowie od lat mają problemy z poprawnym zaznaczaniem odcinków i kątów w przestrzeni na maturze z matematyki. Maturzyści postrzegają je jako trudne i omijają temat. Jak się okazuje niesłusznie, gdyż jak wszystko, można te tematy wyćwiczyć i oprzeć się na gotowych schematach.
Największa trudność polega na sporządzeniu odpowiedniego rysunku, zaznaczeniu interesujących nas odcinków, kąta oraz znalezieniu potrzebnych trójkątów prostokątnych. W tym konkretnym zadaniu obiekty nas interesujące są standardowe i często pojawiają się w tego typu zadaniach. Przy dziesiątym, zaczniemy zauważać, że praktycznie zawsze każą zaznaczyć to samo i policzyć te same rzeczy.
Sporządzamy rysunek i wprowadzamy oznaczenia:
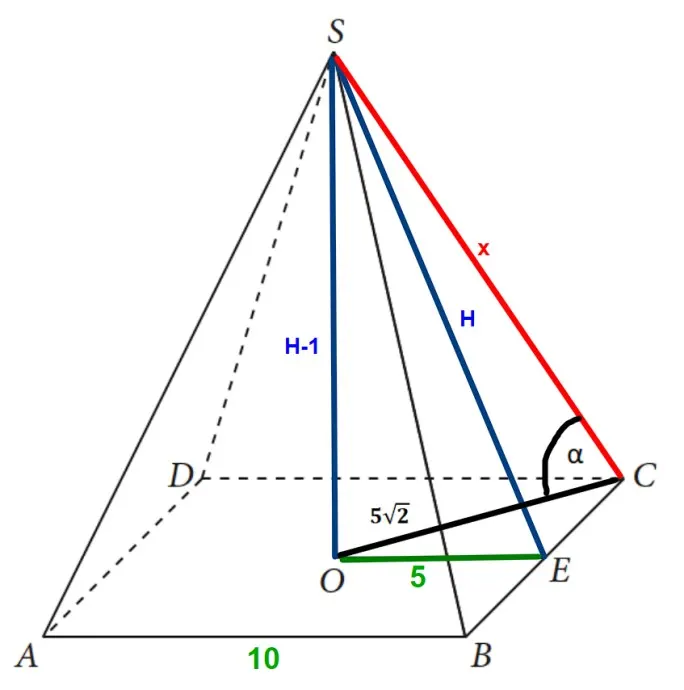
Odcinek |OC|= 5\sqrt{2} 5√2 ponieważ jest to połowa przekątnej kwadratu. Odcinek |OE|= 5 ponieważ jest to połowa długości boku |AB|. Zaznaczamy trójkąty prostokątne OES i OCS. Kąt α jest iterującym nas kątem pomiędzy krawędzią boczną, a płaszczyzną podstawy. Pozostałe oznaczenia wysokości wynikają z treści zadania.
Z funkcji trygonometryczny dla trójkąta prostokątnego wiemy, że: