Stale, a zwłaszcza w tym gorącym okresie, ósmoklasiści powinni być wspierani przez wszystkich, którzy są w stanie im w jakikolwiek sposób pomóc. W tym gronie nie może zabraknąć również wydawnictwa Nowa Era, które swoimi inicjatywami wspomaga i uczniów, i nauczycieli. Jedną z nich jest Diagnoza Nowej Ery, w ramach której przeprowadzane są corocznie próbne egzaminy. W tym artykule zostaną omówione wyniki ostatniego z nich (jesień 2024). Następnie przedstawione zostaną pewne sugestie i pomysły ‒ jak przygotowywać ósmoklasistów do właściwego egzaminu ‒ głównie pod kątem sprawnej organizacji powtórek i unikania błędów podczas rozwiązywania zadań.

Nim jednak te kwestie zostaną omówione, warto krótko przypomnieć najważniejsze zmiany w egzaminie ósmoklasisty z matematyki, które czekają uczniów w 2025 roku.

Zmiany w egzaminie ósmoklasisty 2025

Od roku 2025 egzamin ósmoklasisty jest przeprowadzany

• na podstawie wymagań określonych w wymaganiach ogólnych i szczegółowych podstawy programowej kształcenia ogólnego zawartych w Rozporządzeniu Ministra Edukacji z dnia 28 czerwca 2024 r.;
• w oparciu o Informator o egzaminie ósmoklasisty od roku szkolnego 2024/2025.

Arkusz egzaminacyjny będzie zawierał:

• 14-15 zadań zamkniętych (14-15 punktów)
• 5-6 zadań otwartych (15-16 punktów)

czyli razem 20-21 zadań, za które będzie można otrzymać łącznie 30 punktów.

W porównaniu z egzaminami, które były przeprowadzane przez kilka ostatnich lat:

• liczba zadań otwartych wzrasta z 4 do 6;
• liczba punktów za cały arkusz zwiększa się z 25 do 30;
• zrezygnowano z zadań otwartych za 4 punkty, które zgodnie z poprzednią wersją Informatora mogły wystąpić w arkuszu (w latach 2019-2024 nie było takich zadań);
• zwiększono ilość czasu przeznaczonego na rozwiązanie zadań ze 100 minut do 125 minut.

Jak skorzystać z diagnozy Nowej Ery? – egzamin ósmoklasisty z matematyki

Każdą diagnozę edukacyjną można określić jako zespół działań prowadzonych w środowisku nauczania, mających na celu rozpoznanie, ocenę i projekcję poprawy efektywności procesu dydaktycznego. Dlatego powinna być ona wszechstronna, pokazująca zastany stan w wielu przekrojach i dostarczająca praktycznych informacji niezbędnych do projektowania dalszych działań. I taką jest diagnoza Nowej Ery.

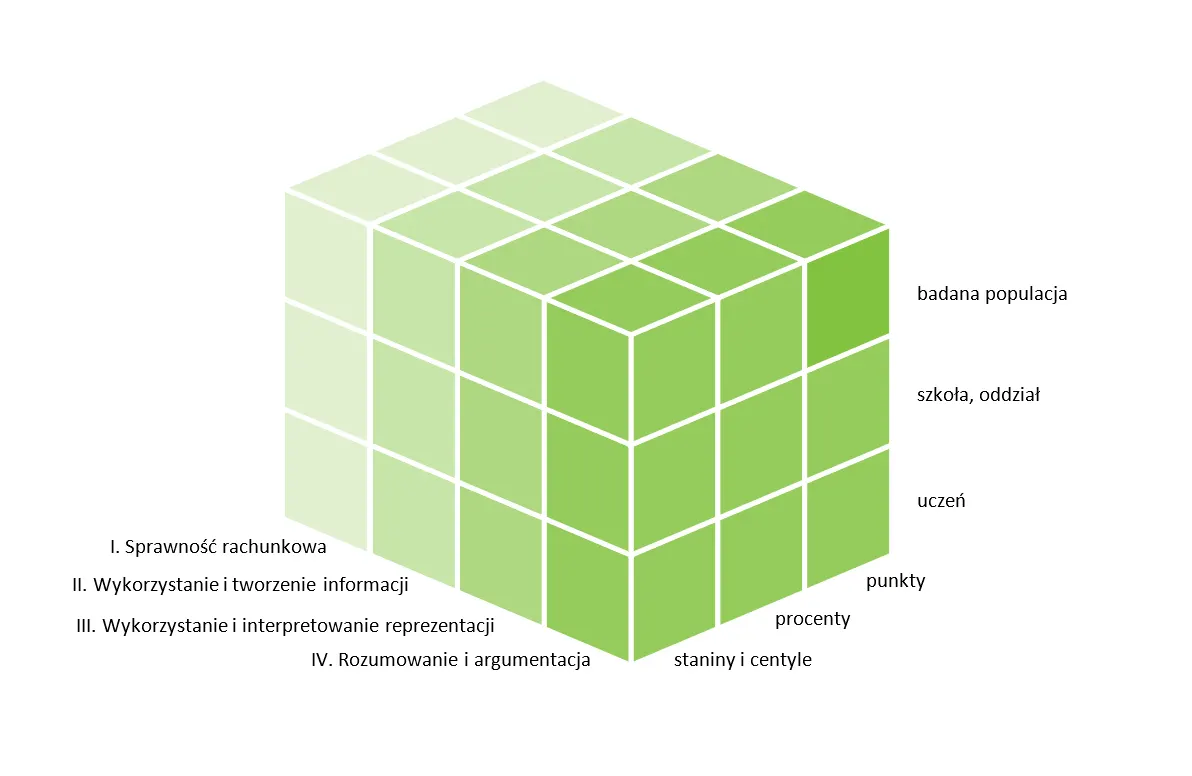
Na schemacie 3D widać trójpłaszczyznowy układ przenikających się obszarów. Pierwszy z nich, to cztery umiejętności ogólne zamieszczone w podstawie programowej. Drugi, to przekrój ze względu na populację, której wyniki są statystycznie opracowywane: ogół objętych diagnozą, szkoła i klasa oraz pojedynczy uczeń. Trzeci związany jest z formą prezentacji uzyskanych wyników: punkty, procenty, staniny i centyle. Jak widać, jest to rozpoznanie bardzo szczegółowe, dające możliwość realnej oceny poziomu kompetencji uczniów.\

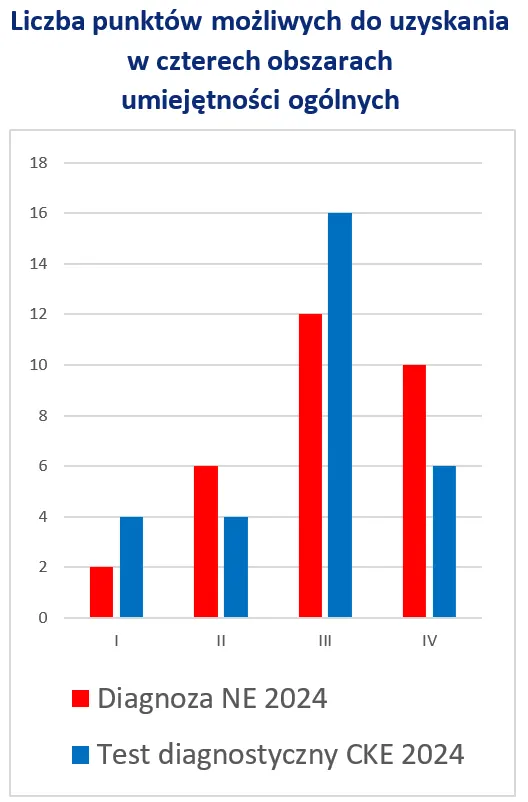
Warto zwrócić uwagę, że arkusz próbnego egzaminu ósmoklasisty z matematyki Nowej Ery z listopada 2024 r. ma strukturę analogiczną do arkuszy CKE (diagram obok):

• w podobnym zakresie bada opanowanie umiejętności ogólnych z czterech obszarów wyróżnionych w podstawie programowej,
• proporcje dotyczące liczby zadań oraz liczby możliwych do uzyskania punktów są zbliżone.

A zatem wyniki uzyskane podczas listopadowej próby są dobrą antycypacją tego, czego można się spodziewać na właściwym egzaminie. Wystarczy jedynie wykorzystać kilkumiesięczny okres, który pozostał, na uzupełnienie ewentualnych braków, które ta próba zasygnalizowała.

Wyniki diagnozy – analiza najłatwiejszych i najtrudniejszych zadań z matematyki

Na kolejnych diagramach zaprezentowane są wyniki uzyskane przez  całą populację objętą diagnozą. Rozkład wyników procentowych jest wyraźnie prawoskośny, czyli przeważają wyniki słabsze. Jest to ważna informacja, pobudzająca do określonych działań, ale należy ją czytać lokując na osi czasu. Do egzaminu ósmoklasisty z matematyki było wówczas jeszcze pół roku, zatem przygotowania do egzaminu dopiero wchodziły w bardziej intensywną fazę, a z uczniowskiej perspektywy półroczny okres to bardzo dużo czasu i ‒ co za tym idzie ‒ motywacja do powtórek nie osiągała wtedy zbyt wysokiego poziomu.

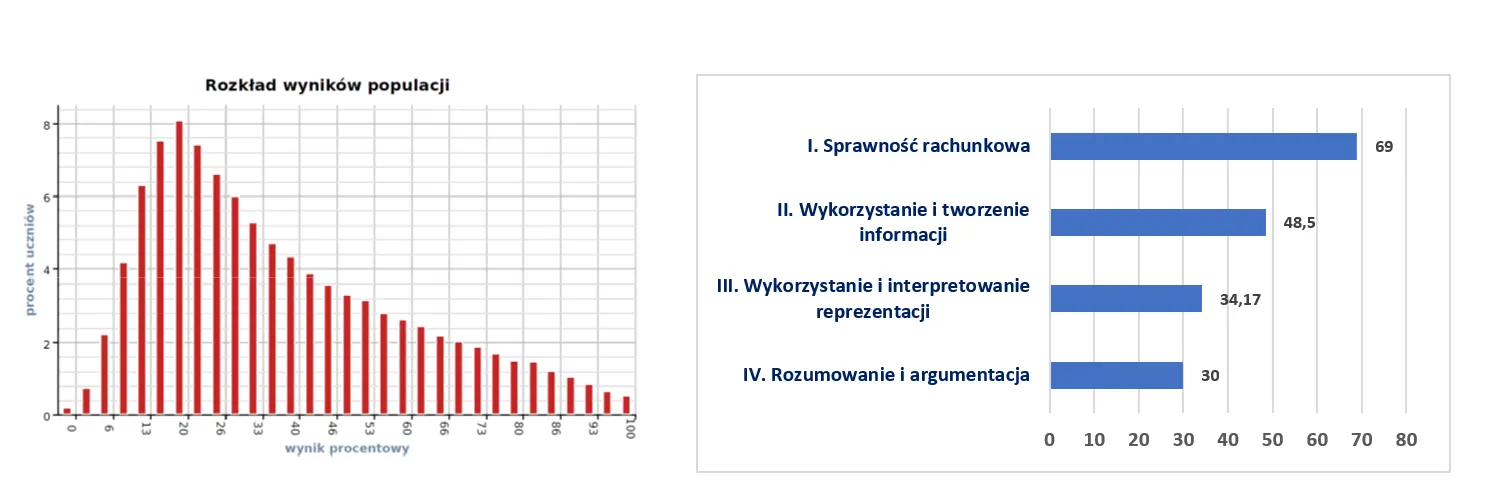
Wyniki procentowe dla czterech kompetencji ogólnych w swoich proporcjach nie odbiegają od tych, które osiągane są na właściwym egzaminie przeprowadzanym przez CKE. Uczestnicy listopadowej próby wykazali się niezłą sprawnością rachunkową, przeciętnym poziomem opanowania umiejętności wykorzystywania i tworzenia informacji oraz wykorzystania i interpretacji informacji i słabo opanowanymi kompetencjami w zakresie rozumowania i argumentacji.

Więcej szczegółowych spostrzeżeń można poczynić, analizując najłatwiejsze i najtrudniejsze zadania z jesiennej diagnozy Nowej Ery.

Najłatwiejszym okazało się zadanie sprawdzające sprawność rachunkową, dotyczące znajomości cech podzielności. Rozwiązalność tego zadania wynosiła 82%.

Podobny poziom trudności reprezentowało zadanie związane z rozumieniem wielkości wprost proporcjonalnych. Tu rozwiązalność osiągnęła wartość 76%.

Próbny egzamin ósmoklasisty z matematyki – co sprawiało największą trudność?

Przechodząc do prezentacji najtrudniejszych zadań z próbnego zestawu egzaminacyjnego z matematyki, warto zwrócić uwagę nie tylko na kwestie formalne (umiejętności ogólne, punktowanie rozwiązania), ale również na te umiejętności szczegółowe, które najprawdopodobniej nie są jeszcze w dostatecznym stopniu opanowane, czyli na główną przyczynę niskich osiągnięć.

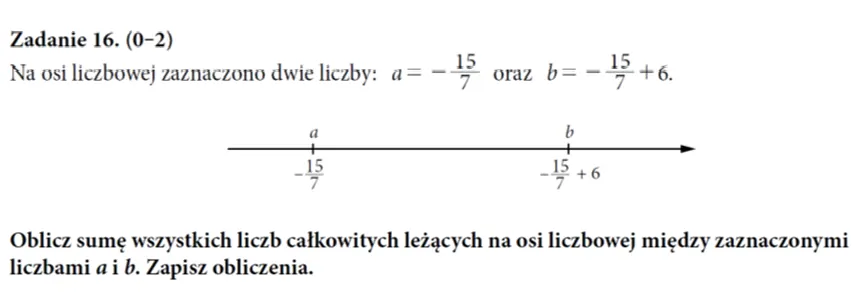
Najtrudniejszym zadaniem w całym zestawie okazało się to, w którym uczeń miał się wykazać umiejętnością posługiwania się osią liczbową. Jego rozwiązalność, to zaledwie 12%.

Punktowane czynności: wyznaczenie wszystkich liczb całkowitych leżących na osi liczbowej między liczbami a i b, obliczenie sumy wszystkich liczb całkowitych leżących na osi liczbowej między liczbami a i b.

Umiejętności słabo opanowane (przypuszczalnie): zamiana ułamka niewłaściwego na liczbę mieszaną, zaznaczanie niecałkowitej liczby ujemnej na osi liczbowej, dodawanie liczb ujemnych i dodatnich.

Niewiele łatwiejsze było zadanie dotyczące drogi, prędkości i czasu, czyli obliczeń praktycznych z poziomu klas IV-VI. Za rozwiązanie tego zadania przyznano jedynie 15% punktów możliwych do zdobycia.

Punktowane czynności: zastosowanie poprawnego sposobu obliczenia długości trasy, zastosowanie poprawnego sposobu obliczenia czasu jazdy w dół. obliczenie czasu jazdy w dół.

Umiejętności słabo opanowane (przypuszczalnie): obliczanie jednej z trzech wielkości: prędkość, droga, czas w ruchu jednostajnym, gdy dwie pozostałe są dane, dostrzeganie zależności wprost proporcjonalnych, zamiana jednostek.

Zadania geometryczne też przysporzyły uczniom sporo kłopotów. To, które jest zaprezentowane obok, osiągnęło rozwiązalność 25%, a dotyczyło nietrudnej umiejętności obliczania obwodu wielokąta i z pewnością dobrze ćwiczonej umiejętności stosowania twierdzenia Pitagorasa.

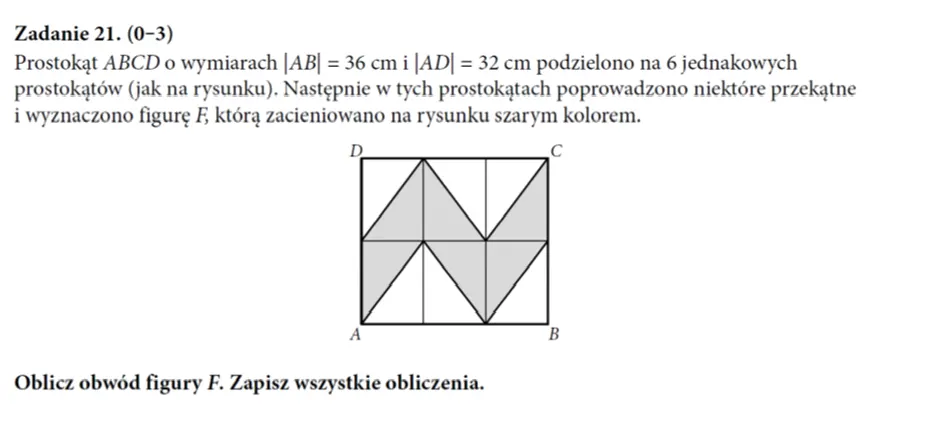
Punktowane czynności: zastosowanie poprawnego sposobu obliczenia wymiarów małego prostokąta, zastosowanie poprawnego sposobu obliczenia długości przekątnej małego prostokąta, obliczenie obwodu figury F.

Umiejętności słabo opanowane (przypuszczalnie): odczytywanie informacji z rysunku, stosowanie twierdzenia Pitagorasa, obliczanie obwodu wielokąta, opracowanie strategii rozwiązania.

Punktowane czynności: obliczenie rzeczywistych wymiarów basenu lub obliczenie obwodu basenu, obliczenia skali, w której został sporządzony nowy plan.

Umiejętności słabo opanowane (przypuszczalnie): obliczanie rzeczywistych wymiarów prostokąta, gdy znane są jego wymiary w danej skali, obliczanie skali planu, obliczanie obwodu prostokąta.

Nieco tylko łatwiejsze okazało się zadanie dotyczące obliczeń związanych ze skalą opisanych w części podstawy programowej dla klas IV-VI. Za jego rozwiązanie przyznano jedynie 28% punktów, które można było osiągnąć.

30% punktów możliwych do uzyskania przyznano za rozwiązanie tego zadania. Mogło ono rzeczywiście stwarzać uczniom pewne trudności, gdyż łączyło umiejętności wykonywania działań na ułamkach (poziom IV-VI) i rozwiązywania równań (poziom VII-VIII), a także wymagało zbudowania odpowiedniego modelu matematycznego.

Punktowane czynności: zastosowanie poprawnego sposobu obliczenia długości części listewki po pierwszym podziale, zastosowanie poprawnego sposobu obliczenia długości części listewki po drugim podziale, obliczenia długości otrzymanych trzech części listewki.

Umiejętności słabo opanowane (przypuszczalnie): porównywanie ilorazowe i różnicowe, modelowanie (geometryczne lub algebraiczne), uważne czytanie treści zadania.

Punktowane czynności: określenie miary kąta przy podstawie w jednym z trójkątów równoramiennych: ABC lub CDE, obliczenie miary kąta BCD.

Umiejętności słabo opanowane (przypuszczalnie): odczytywanie informacji z rysunku, znajomość własności trójkątów równoramiennego i równobocznego.

Trzydziestoprocentową rozwiązalność osiągnęło również to, wydawałoby się nietrudne, zadanie z planimetrii. Do jego rozwiązania wystarczyło znać twierdzenie o sumie kątów wewnętrznych trójkąta i własności trójkątów równoramiennych.

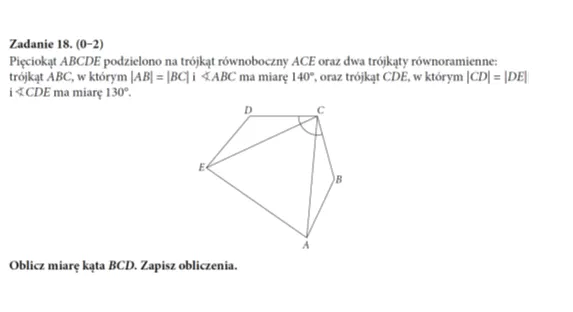
Ostatnim z serii najtrudniejszych jest zadanie zamknięte na dobieranie typu „tak-nie, ponieważ”. Jedynie co trzecia osoba poprawnie wskazała właściwą odpowiedź. Dotyczyło ono, co prawda, trudnego dla uczniów materiału, bo szacowania wartości pierwiastków, ale sama struktura zadania niewątpliwie mogła pomóc.

Umiejętności słabo opanowane (przypuszczalnie): rozumienie zależności: przyczyna-skutek, umiejętność szacowania wartości pierwiastka kwadratowego.

Najtrudniejsze zadania z matematyki – podsumowanie

Tytułem podsumowania stwierdzić można, że:

• 6 najtrudniejszych zadań ma rozwiązalność poniżej 34%.
• 2 najtrudniejsze dotyczą umiejętności:
  • III. Wykorzystanie i interpretowanie reprezentacji.
  • Używanie prostych, dobrze znanych obiektów matematycznych, interpretowanie
    pojęć matematycznych i operowanie obiektami matematycznymi.

• 3 kolejne dotyczą umiejętności:
  • Rozumowanie i argumentacja.
  • Stosowanie strategii wynikającej z treści zadania, tworzenie strategii rozwiązania
    problemu, również w rozwiązaniach wieloetapowych oraz w takich, które wymagają umiejętności łączenia wiedzy z różnych działów matematyki.

• 4 najtrudniejsze zadania dotyczą materiału realizowanego w klasach 4-6.

Jak unikać błędów podczas rozwiązywania zadań z matematyki na egzaminie ósmoklasisty?

Powodów błędów jest bardzo wiele, a co za tym idzie, wiele jest także sposobów na ograniczenie ich pojawiania się. Tu, na kanwie zadań CKE oraz wybranych z publikacji Nowej Ery, przedstawionych zostanie kilka częściej występujących sytuacji.

Błędna interpretacja rysunku

To częsty powód udzielania błędnej odpowiedzi lub niewłaściwego prowadzenia rozwiązania zadania. Nierzadko zdarza się, że nie wszystkie istotne informacje znajdują się w tekście zadania i trzeba je odnaleźć, odczytać z rysunku, diagramu, czy schematu.

Umiejętność zauważania związków między elementami graficznego modelu sytuacji opisanej w zadaniu jest złożoną kompetencją, wymagającą wielu ćwiczeń, stosunkowo wysokiego poziomu wiedzy z danego obszaru, a także rozwiniętych zdolności poznawczych: spostrzegawczości, myślenia analitycznego, dostrzegania relacji. Pobieżna, niepełna umiejętność analizy i interpretacji graficznego przedstawienia informacji prowadzi bardzo często do niepoprawnych rozwiązań, czy złych odpowiedzi. Dostrzec to można na trzech poniższych przykładach.

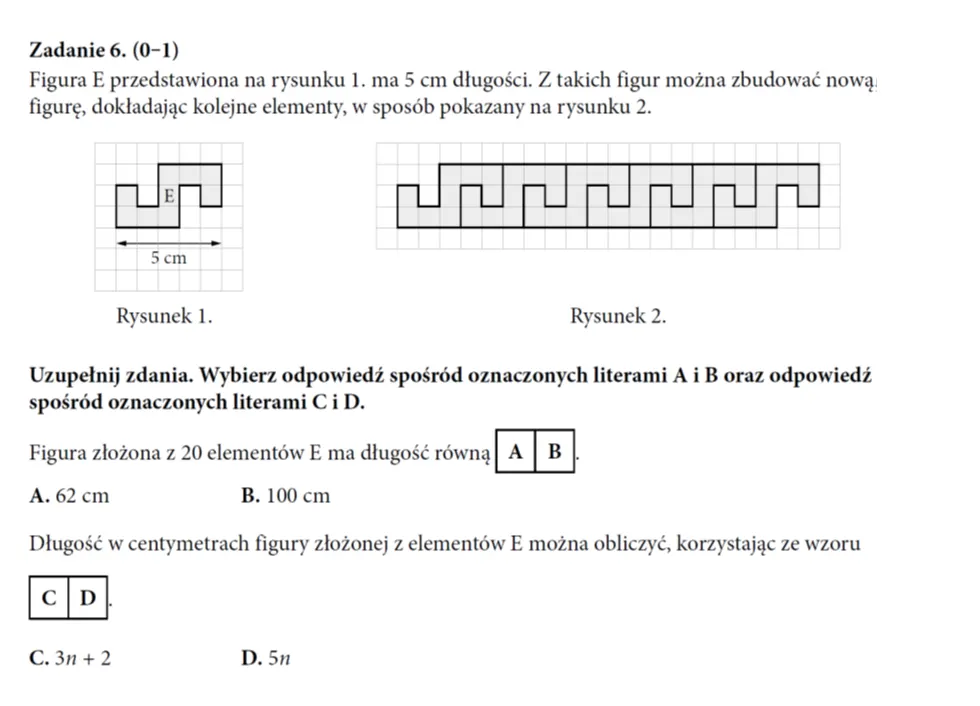
• W zadaniu zamieszczonym obok pochopne skojarzenie, że jeśli jeden element ma długość 5 cm, to figura złożona z 20 takich elementów ma długość
  20 · 5 cm = 100 cm jest oczywiście błędne, chociaż pojawiające się stosunkowo często. Konsekwencją wyboru B w pierwszym zdaniu jest wybór D w drugim. Oba oczywiście niepoprawne, bo przecież dołożenie kolejnego elementu do budowanej figury nie powoduje jej wydłużenie o 5 cm, lecz o 3 cm.

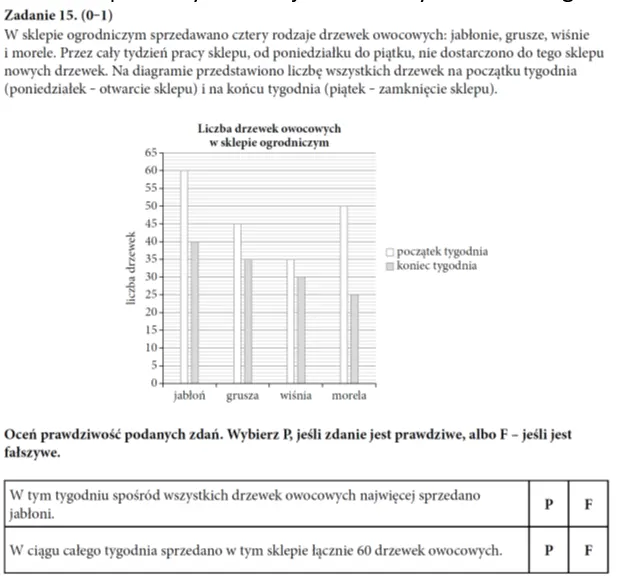
• W tym zadaniu łatwo błędnie zinterpretować dane przedstawione na diagramie. Oceniając poziom sprzedaży jabłoni uczeń może błędne zasugerować się tym, że biały słupek dotyczący jabłoni jest najwyższy i stwierdzić, że pierwsze zdanie jest prawdziwe. Tymczasem o wielkości sprzedaży informuje różnica wysokości białego i szarego słupka, a ta jest najwyższa w przypadku moreli.

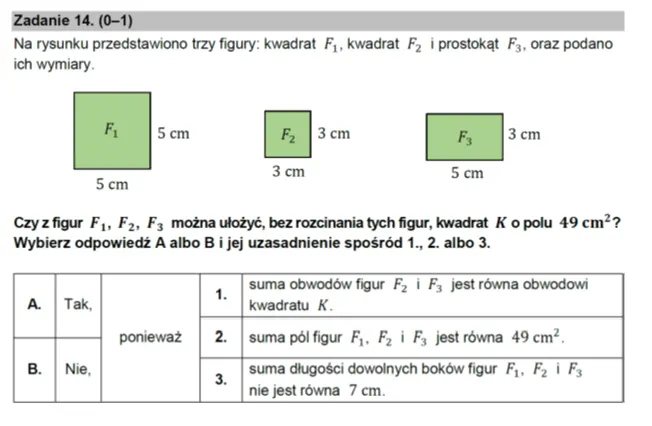
• Tu przyczyną błędnej odpowiedzi może być niewłaściwa analiza informacji o figurach zapisanych na rysunku. Rzeczywiście, suma pól tych trzech figur jest równa polu kwadratu , a suma obwodów figur i  jest równa obwodowi tego kwadratu. Ale to nie jest informacja rozstrzygająca możliwość wykonania czynności opisanej w zadaniu. Dopiero próby zbudowania kwadratu  podjęte z uwzględnieniem wymiarów danych figur, a właściwie ich nieskuteczność, daje szansę na sformułowanie poprawnej odpowiedzi.

Nieznajomość definicji

Umiejętności matematyczne związane są z rozumowaniem, interpretowaniem, wnioskowaniem i innymi czynnościami intelektualnymi, ale muszą się odbywać z udziałem obiektów jednoznacznie określonych, stąd znajomość definicji jest niezbędnikiem warunkującym poprawność postępowania podczas rozwiązywania zadania. Dwa poniższe przykłady pokazują, jak jest to ważne.

Zadanie jest nietrudne, wymaga prostych obliczeń. Jest tylko jedno „ale” ‒ trzeba wiedzieć, jakie kąty nazywamy przyległymi. I nie wystarczy tu intuicja wynikająca z nazwy („przylegają do siebie”), ale niezbędne jest precyzyjne określenie położenia takich kątów opisane właśnie w ich definicji.

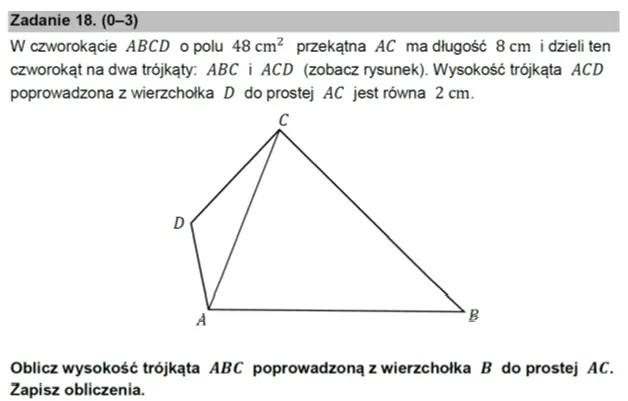
Obiektem, którego określenie ‒ do końca precyzyjne trzeba znać, aby rozpocząć pracę nad tym zadaniem jest wysokość trójkąta. To zadanie jest trudniejsze (otwarte, 3-punktowe), czyli do rozwiązania dochodzi się w kilku krokach. Tym ważniejsza jest dokładna znajomość pojęć, które występują w przedstawionej sytuacji geometrycznej. Błąd wynikający z pełnej lub częściowej nieznajomości pojęć, którymi trzeba operować (błędne poprowadzenie wysokości lub uznanie za wysokość odcinka, który nią nie jest) popełniony zwłaszcza na początku procesu rozwiązywania może sprawić, że całe następujące po nim rozwiązanie nie zostanie zaakceptowane, a uczeń, gdy taka sytuacja wydarzy się na egzaminie, straci punkty i czas.

Niewłaściwe analogie, błędne stosowanie wzorów

Te dwie przyczyny, niekiedy powiązane ze sobą, są bardzo częstymi źródłami błędnych rozwiązań.

• Zadanie przedstawione obok jest nietrudnym ćwiczeniem z obliczania wartości pierwiastka będącej liczbą wymierną. Zwłaszcza w pierwszej części zadania „kuszące” wartości: 1 i skłaniają osoby mające słabo opanowane umiejętności działania na pierwiastkach do pierwiastkowania „po kawałku”, czyli wyliczanie oddzielnie pierwiastka z 1 i pierwiastka z       .

• W tym zadaniu jeszcze wyraźniej widać, jak pokusa stosowania nieuprawnionych analogii prowadzi do błędu: skoro iloczyn ułamków otrzymujemy mnożąc licznik przez licznik i mianownik przez mianownik, to dodawanie pewnie też tak można wykonać. Oczywiście, nie można, ale ten błąd jest mocno zakorzeniony w umysłach wielu uczniów.

Jak ograniczyć błędy podczas rozwiązywania zadań na egzaminie ósmoklasisty? - wnioski

Wracając do wcześniej sformułowanego pytania: co robić, aby było mniej błędów w rozwiązaniach zadań na egzaminie, warto wykorzystać sugerowane niżej działania, które z pewnością mogą wspomóc inne działania nauczycieli.

Braki w wiedzy faktograficznej, „półwiedza”, ubogi zasób metod, brak umiejętności technicznych:

• ćwiczyć czytanie ze zrozumieniem tekstów matematycznych, rysunków, wykresów;
• ustalić genezę błędu;
• wrócić do momentu wprowadzenia tej wiedzy;
• wykorzystać właściwe analogie (np. algebra – arytmetyka);
• wskazać możliwość wykorzystania narzędzi z innego działu;
• stosować „burzę mózgów” – poszukiwanie alternatywnych sposobów rozwiązań;
• wzmóc motywację uczniów.

Brak doświadczenia w rozwiązywaniu bardziej złożonych problemów:

• zacząć od rozwiązań wymagających 2-3 kroków;
• napisać plan rozwiązania zadania;
• używać wizualizacji (grafy, rysunki, schematy, mapy myśli);
• czytać rozwiązania w podręcznikach i innych książkach;
• zachęcić uczniów do ułożenia i rozwiązania analogicznego zadania.

Słabo rozwinięta umiejętność myślenia abstrakcyjnego:

• zacząć od konkretów;
• stopniowe abstrahowanie (model – rysunek – wyobrażenie);
• przed posłużeniem się obiektem abstrakcyjnym sprawdzać poprawność
  jego rozumienia (pytania ogólne, ale związane z kontekstem zadania).

 Trudności ze zrozumieniem, niska motywacja ‒ sugestie dla uczniów:

• staraj się zrozumieć powtarzany materiał;
• trudny materiał powtarzaj tak, jakbyś tłumaczył to innej osobie;
• nie ucz się na pamięć (oprócz niezbędnych wzorów i reguł);
• analizuj swoje błędy, ustal ich przyczyny;
• myśl pozytywnie, uwierz w swoje możliwości;
• wyznaczaj sobie drobne nagrody.

Wiele interesujących wskazówek można znaleźć w corocznych sprawozdaniach Centralnej Komisji Egzaminacyjnej zawierających szczegółowe omówienie ostatniego egzaminu ósmoklasisty z matematyki. Oto kilka wybranych rekomendacji:

• ćwiczenie umiejętności odczytywania informacji przedstawionych w różnej formie;
• wykorzystanie szacowania wartości do sprawdzenia poprawności;
• wyrabianie nawyku sprawdzania otrzymanego wyniku z warunkami zadania;
• zachęcanie do rozwiązywania problemów matematycznych różnymi sposobami;
• wyszukiwanie i rozwiązywanie na lekcjach problemów praktycznych;
• ćwiczenie umiejętności budowania modelu matematycznego dla danego kontekstu;
• pokazywanie przykładów rozwiązań uczniowskich, w których błąd w obliczeniach uniemożliwił skuteczne doprowadzenie rozwiązania do końca.

 Jak skutecznie zorganizować powtórki i jak efektywnie wykorzystać czas na egzaminie – podpowiedzi dla nauczycieli i ósmoklasistów

Dobre zorganizowanie powtórek, to połowa sukcesu. Projektując je, warto pamiętać, aby:

 Zdiagnozować uczniowską wiedzę i niewiedzę:

• przeanalizować podstawę programową,
• przeprowadzić próbny egzamin.

 Opracować harmonogram powtórek:

• oszacować ilość czasu do dyspozycji,
• określić umiejętności, których powtórzenie wymaga więcej czasu,
• podzielić cały materiał na mniejsze moduły,
• zaplanować terminy powtórek kompleksowych,
• uwzględnić powrót do wcześniej powtarzanych treści.

 Zaplanować sposoby monitorowania postępów:

• rozwiązywać krótkie testy tematyczne,
• notować typowe błędy i trudności,
• oceniać postępy,
• mierzyć czas na rozwiązanie arkuszy ćwiczeniowych.

 Zgromadzić potrzebne materiały:

• adresy stron internetowych,
• publikacje książkowe:
  • podręczniki,
  • Repetytorium,
  • Arkusze ćwiczeniowe,
  • Tablice matematyczne.

  Nawiązać kontakt z osobami, które mogą pomóc:

• nauczyciele:
  • inne osoby uczące matematyki,
  • pedagog szkolny,
  • doradca metodyczny;

• uczniowie:
  • koleżanki i koledzy z klasy,
  • osoby, które niedawno zdawały egzamin ósmoklasisty.

Jak efektywnie wykorzystać 125 minut egzaminu ósmoklasisty z matematyki – porady dla uczniów

Oto mini-poradnik dla zdających.

 Przed egzaminem z matematyki:

• Przeanalizuj strukturę arkuszy pod kątem:
  • budowy arkusza (wkładka z zadaniami otwartymi),
  • liczby zadań zamkniętych i ich rodzajów oraz sposobu zaznaczania rozwiązania w karcie odpowiedzi i korygowania błędów,
  • liczby zadań otwartych i liczby punktów, które można uzyskać za ich rozwiązanie.
• Rozwiązuj arkusze próbne w czasie 125 minut, naucz się decydować, czy kontynuować pracę nad zadaniem, które „nie wychodzi”, czy przejść do następnego.

 Podczas egzaminu z matematyki:

• Przejrzyj szybko cały arkusz:
  • zaznacz zadania, które potrafisz rozwiązać od razu,
  • oszacuj, ile czasu będziesz potrzebował na rozwiązanie zadań otwartych.

• Pracuj ekonomicznie:
  • podczas rozwiązywania  zadań sprawdzaj, ile czasu pozostało do końca,
  • zacznij od zadań najłatwiejszych,
  • jeśli nie masz pomysłu na rozwiązanie zadania, nie przedłużaj pracy nad nim, przejdź do następnego, a do tego wróć, gdy zostanie ci czas,
  • zarezerwuj 5-10 minut na końcowe przejrzenie wszystkich rozwiązań, sprawdź, czy wszystkie odpowiedzi zaznaczone są na karcie odpowiedzi.

• Opanuj stres:
  • zachowaj spokój, racjonalnie wykorzystaj czas, jaki pozostał do końca,
  • w razie potrzeby zrób krótką przerwę, rozpręż się, weź kilka głębokich oddechów.

Egzamin ósmoklasisty to ważny moment sprawdzenia nie tylko uczniowskiej wiedzy, ale także umiejętności logicznego myślenia i stosowania matematyki w praktyce. Jest także okazją do pokazania, jak nasi podopieczni potrafią radzić sobie z problemami i stresującymi sytuacjami. Każdy wysiłek włożony w przygotowania do tego ważnego wydarzenia, to krok do poczucia satysfakcji z osiągnięcia sukcesu.